The Kroleski home is one that enjoys boardgames. We’re a fun loving kind of people. My wife & I are both very competitive though – so things can get a bit intense when we start playing. In order to get the upper hand for our game nights – I’m starting a new series where I use math to look for ways I can increase my chances of winning various board games.

Tonight I’m going to look at a game called Pass the Pigs. We heard about this game from our friends Chris & Gretchen & ended up buying it before our New Zealand trip because it was light weight and we could play it anywhere.

For those who haven’t played before – here are the rules.

This game is perfect for my first ‘Boardgames & Math’ because it is incredibly simple. There is really only one decision to make; should I keep rolling or call it quits. A bit of Googling turned up a number of schools that have used this game to teach students. Whether it was elementary students learning basic probabilities or college CS students learning to program game simulations – this game is popular with teachers.

I’m going to try to expand upon what I’ve seen from most of those courses and see if I can’t solve this game a bit more.  But first, we need some data.

Data Collection

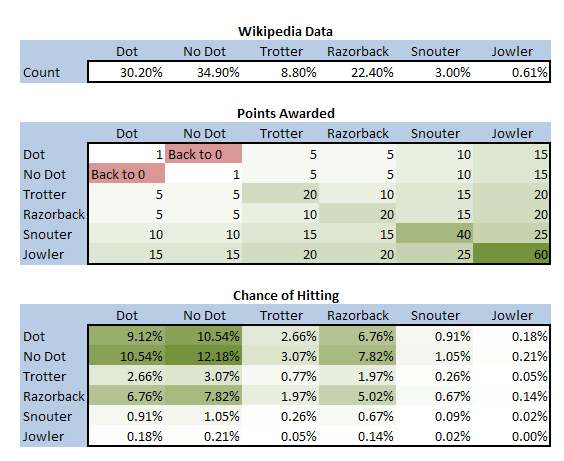
I took a small sample of 210 rolls. The percentages turned out as follows:

Side (Dot) – 26.19%
Side (No Dot) – 33.33%
Trotter – 10.95%
Razorback – 26.67%
Snouter – 2.38%
Jowler – 0.48%

I’m not thrilled with that sample size – as a rule of thumb when testing an unknown it is best to have a count of 20-50 of the smallest number. There is a lot of study about sampling that can pinpoint more exact numbers – either way, I don’t have time to roll these pigs a few thousand times tonight.

Thankfully someone else did this and published the results to wikipedia – I’m not sure their pigs are exactly the same as mine – but from comparing the probabilities, they seem at least similar. I am going to use their numbers to build my models and will loop back and replace my variables later using data from the results of future games with my set of pigs.

Possible Scenarios

Because Pass the Pigs scores you based on the combination of two pigs – we must multiply out the percentages to find the chance that each scenario will occur. Below I’ve included the point value and probability of each scenario in two tables.

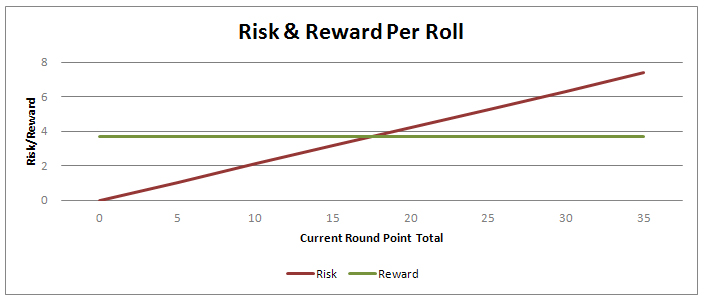
Risk & Reward

The interesting aspect of this game is that the reward for each roll is fixed but the risk is dependent upon how many points you have accumulated during your current round. On your first roll, you have 0 points, so there is no risk to rolling, the worst case scenario is that you end up with 0 which is where you are now anyways. If, however, you have 25 points accumulated this round, rolling again would put all of those at risk.

We can quickly get an idea of when the break-even roll occurs by multiplying out the potential rewards by the probability of hitting them. It turns out when you multiply all of the positive results from those two tables above you find out that there is a 78.92% chance your result will be positive and the mean reward for that will be 4.71 points.

At the same time, there is a 21.08% chance you will ‘pig out’ and be set back to 0 for the round. When you multiply that by your current points you will find your current probable risk.

Because the reward is fixed and the risk increases with your accumulated score you will eventually hit a point where the probable risk is greater than the probable reward and it will no longer be mathematically wise to keep rolling.

It turns out this happens when you have about 17.64 points. You can find this algebraically by doing X = (P{reward} * AVG(reward})/P{risk}. Where P is probability & AVG is the mean reward. It looks like this.

Now there are actually a few caveats that I think will be important here. The distribution of the rewards is fairly spread out and each roll allows the player a chance at another roll, so I don’t think the math will end up being quite as simple as I’ve described above. Unfortunately, we are bumping into the limits of my probability theory knowledge here so I’m going to switch from solving it with math to using brute force & doing a bit of programming.

Letting The Computer Do The Heavy Lifting

What we are going to do is create some code to simulate the game and then play it a few thousand times, changing various aspects of our strategy as we go, trying to see what works best.

You can continue to read about that here in part 2.